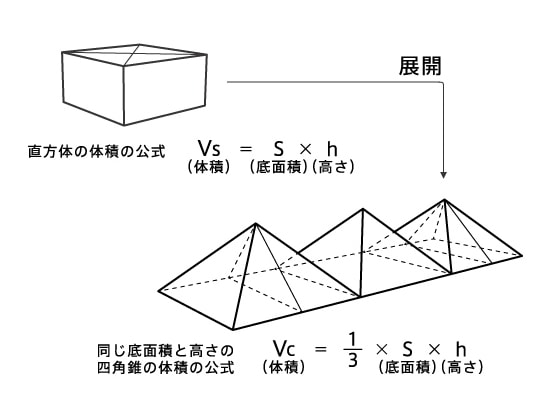
に,体積が求められるようにする。 活動の流れ 数学的な考え方 学習活動 2 帰納的に推論する ① 円柱と円錐,四角柱と四角錐の体積の関係 から,同じ底面積で同じ高さをもつ立体の体 積の関係を類推する。 ↓ 1 類推する 三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。 ④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。
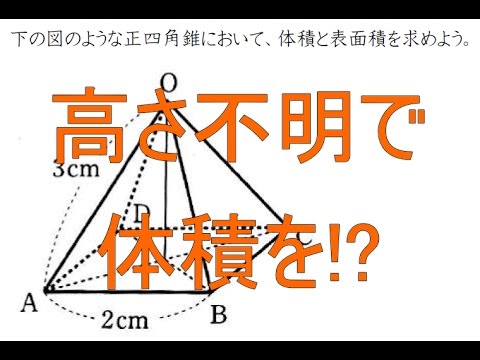
この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋
角錐の体積なぜ1 3
角錐の体積なぜ1 3-四角錐の体積=(35)÷2×4×6÷3=32cm 3 です。 角錐の体積の公式は?1分でわかる公式、柱体の体積との違い、3分の1になる証明体積はどちらも 『体積=底面積×高さ×1 3 1 3 』 となります。 このときの "高さ" とは、 頂点から底面に下ろした垂線の長さ です。 角柱や円柱の場合体積は「底面積×高さ」でしたが、錐体の場合これに 1 3 1 3 をかけます。




この体積と表面積の求め方を教えてください Clear
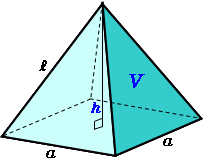
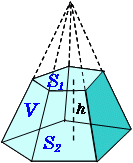
角錐,円錐の体積 底面積が ,高さが の円錐や角錐(三角錐,四角錐,五角錐,・・)の体積は, (底面積×高さ) で表わされます。 特に円錐では,底面の半径をrとすると だから になります。 三角錐,四角錐,円錐,の錐 (すい)という漢字は訓読みでは「きり」と読みます.これは,小さな穴を開けるための先のとがった工具です. 三角錐や円錐といった「錐」とは,穴をあける道具のように先の尖った立体です. では,「〇〇錐」の体積の求め方はどうだったかというと, (〇〇錐の体積) = (底面積)× (高さ)× 1 3 ( 〇〇錐の体積) = ( 底面積) × ( 高さ) × 1四角錐や五角錐の体積の求め方 忘れている人が割といるので確認しておきます。 柱体と錐体の体積の求め方です。 \(\,\color{red}{(柱体の体積)=(底面積)\times (高さ)}\,\) です。 これは、底面の形に関係なく同じです。 三角柱でも四角柱でも円柱でも同じ。
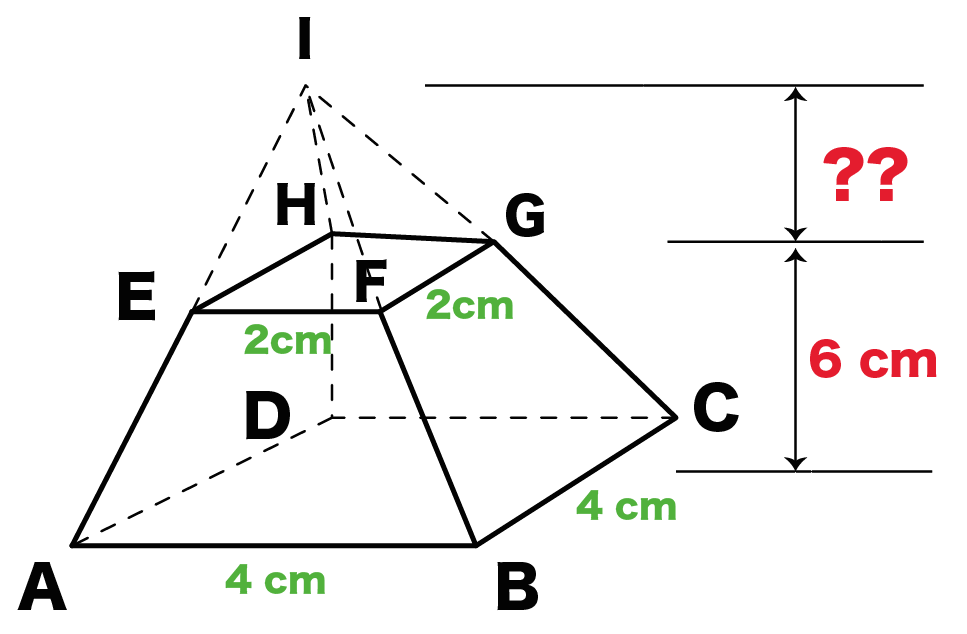
そうすれば「正四角錐台」の体積になる。 さっきの例でいうと、 「正四角錐iabcd」から「正四角錐iefgh」をひけばいいんだ。 地道に計算してやると、 (正四角錐iabcd) (正四角錐iefgh) = 1/3 × ( 66) × 4^2 – 1/3 ×6 × 2^2 = 64 – 8 = 56cm^3 になる。Twitter @tamaki_py https//twittercom/tamaki_pyサムネイル素材:"Pentagonal pyramidpng" (CC BYSA 30) https//commonswikimediaorg/wiki/FilePentagonal日本大百科全書(ニッポニカ) 角錐の用語解説 平面α上に多角形p、αの外に点oがあるとき、oとpの任意の点を結んでできる線分全体のつくる立体を角錐といい、oを頂点、pを底面、底面でない面を側面という。また、oからαに至る距離を高さという。底面の面積がs、高さhの角錐の体積はv=(1/3)s
体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!角柱と角錐の体積を求める公式 角柱と角錐の体積を求めるための公式があります。 角柱の体積=底面積×高さ 角錐の体積=底面積×高さ×1/3 これは円柱や円錐のときも同じで、円柱の体積は、「底面の円の面積×高さ」、円錐の体積は、「底面の円の面積×高 四角錐台の体積は、オベリスク形状を含めた広義で扱っており(上底と下底の長方形が非相似を含む)、体積V=h/6*(AbBa2(abAB))です。なお、ご指摘の体積は上底下底が相似な四角錐台な場合です。⇒関連ライブラリ "角錐台の体積" 1909




角柱と角錐の体積の求め方 中学数学 By じょばんに マナペディア




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体
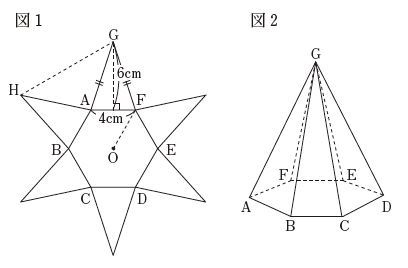



線分hgの長さ 六角錐の体積 中3から質問へのヒント 上北沢 哲英会 個人塾 連絡用ブログ




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
三角錐の体積を求める問題 実際に三角錐の体積を計算しましょう。下図の三角錐の体積を計算してください。 底辺=10cm、高さ=5cm、三角錐の高さcmですね。よって、 三角錐の体積=(5cm×10cm÷2)×cm÷3=1667cm 3 です。正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ




数学 中3 68 三平方 空間図形への利用 角錐編 Youtube
四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。正四角錐の体積(底辺と高さから) 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘ありがとうございます。 修正致し三角すいの内部で、一方向へ縮んだ三角すいの体積は、以下の公式で求めることができます。 全体の体積に、 、 、 をかけたものが、小さい三角すいの体積です。 この 、 、 をかけ合わせた分数が、本講義で"ちぢみ率"と呼んでいるもの。 ちぢみ率は




三平方の定理の利用 四角錐 円錐 チーム エン




円錐や角錐の体積の求め方 中学1年数学 Youtube
正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます.錐の体積 = 底面積 × 高さ× 1 3 高さとは>> 頂点から、底面におろした 垂線の長さのこと。 高さ (例) 底面 9cm 2 高さ 10cm 五角錐 体積=9×10÷3=30 正四角錐(底面が正方形) 4cm 6cm 高さ 底面積=4×4=16 体積=16×6÷3=32 高さ8cm 底面の半径 3cm 円錐 底面積=3×3×π=9π 体積=9π×



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




体積の計算 四角錐 製品設計知識
四角錐の体積は・・・30×4÷3=40 よって上側の立体の体積は6040=100 全体から引くと下側も体積が出せる。 =140 図は∠BAC=90°の直角三角形を底面とする三角柱で、AB=12cm, AC=10cm, AD=15cmとなっている。 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。 今日は、この公式で体積を計算してみよう!! 使って覚えるのが一番だからね。 三角錐の体積の求め方がわかる3ステップ 3ステップで計算できるよ。 底面積をだす; 四角錐の体積=底面積×高さ× 1 3 なので 求める四角錐の体積=36×8× 1 3 =96(cm³) 答え 96cm³




円錐は1 3 中学生に分かるように真剣に考えてみた うちーノート



正四角錐の体積 底辺と側辺から 高精度計算サイト
立体の体積、表面積 問題 ・・・ (む) は難しい問題です。 1 右図の四角錐の底面は1辺の長さ6 (cm)の正方形,側面は等しい辺の長さが2√7 (cm)の二等辺三角形です。 この四角錐の体積は (cm 3 ) ア= イ= この四角錐の表面積は (cm2) ウ= エ= オ= 2 右図は1辺の四角すい 四角錐 体積計算 公式 求め方 高さ 底面積 自動 長方錐 方錐 volume
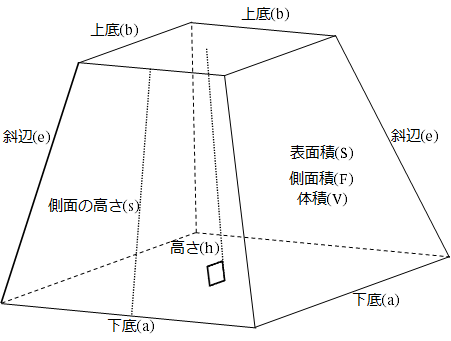



Excelワークシート 正四角錐台の体積や表面積などを計算するワークシート 黒い箱の中




送料無料 ますのび Finden フィンデン volume of a pyramid 四角錐の体積説明器 autumn




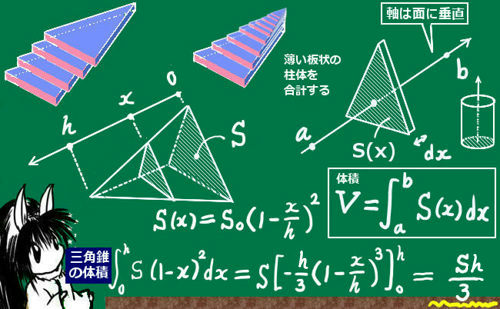
Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703




角錐の体積の求め方 簡単な問題で公式の使い方がわかるよ 中学や高校の数学の計算問題
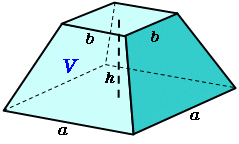



正四角錐台の体積 高精度計算サイト



計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直撃 中学入試 第135回 筑波大附属中 立体 正四角錐の切断 北辰塾 情報局




円錐は1 3 中学生に分かるように真剣に考えてみた うちーノート




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



1




この体積と表面積の求め方を教えてください Clear



1




体積の求め方 計算公式一覧



Volume Of A Pyramid 四角錐の体積説明器 Spring すべての商品 ますのび



Mathematics 立体の切断 高校入試に出る難しい問題 働きアリ



悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



四角錐の体積
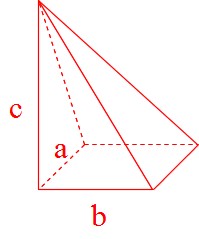



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明
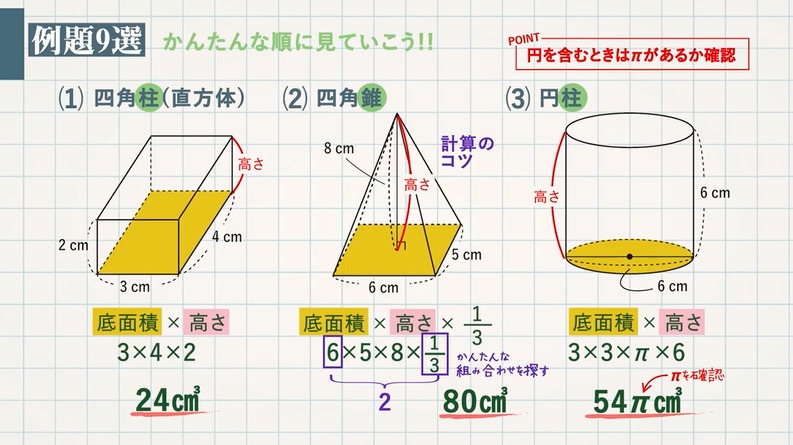



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



角錐台の体積 高精度計算サイト




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




体積の求め方 計算公式一覧



角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明



正四角錐と三平方の定理 中学3年数学 Youtube




数学 中3 54 相似と体積 基本編 Youtube




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学




四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア



答3 四角錐の体積 ヤドカリの 気ままな数学



Q Tbn And9gcteatlk3su2k13ppiy286tged4bmtwyxvgsndquhix Behamia0 Usqp Cau




角錐と円錐の体積 Youtube



立体の体積計算 積分 高校 理数系無料オンライン学習 Kori




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ




角錐 円錐の体積と表面積の公式 数学fun




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




四角錐 円錐の体積 チーム エン



この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋



角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明




四角錐の体積の求め方 公式 小学生 中学生の勉強
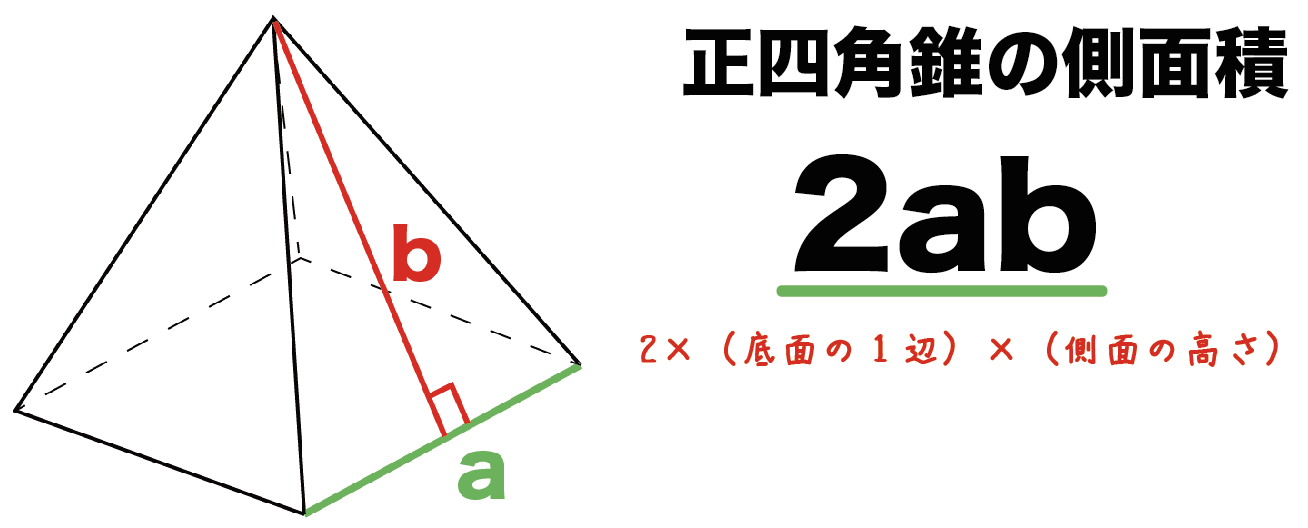



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
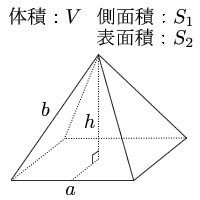



正四角錐 底辺と高さ 体積 表面積の計算 計算サイト




四角錐台の体積 高精度計算サイト
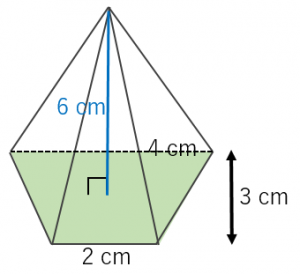



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学
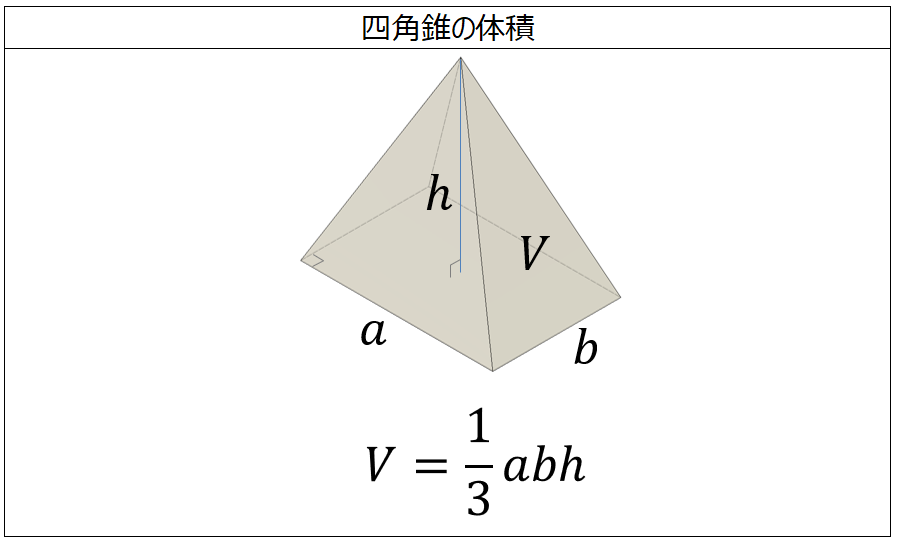



体積の計算 四角錐 製品設計知識




1 16 Cm 1 Descubre Como Resolverlo En Qanda



1




56 四角錐の切断と体積 Youtube
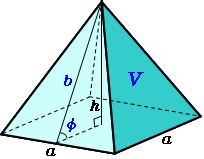



正四角錐の体積 底辺と高さから 高精度計算サイト




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
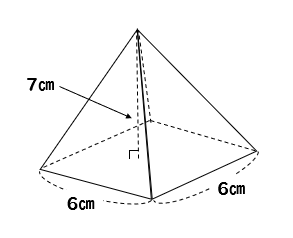



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




一辺の長さがすべて10cmの正三角錐の体積 Clear
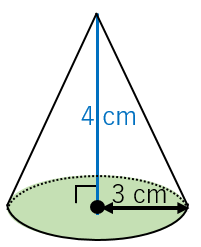



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




どうして1 3なの 錐の体積の公式の求め方 まなべーと




立体の体積 無料で使える中学学習プリント




体積の求め方 計算公式一覧




10 Descubre Como Resolverlo En Qanda



錐の体積




四角錐の体積の求め方 公式 小学生 中学生の勉強
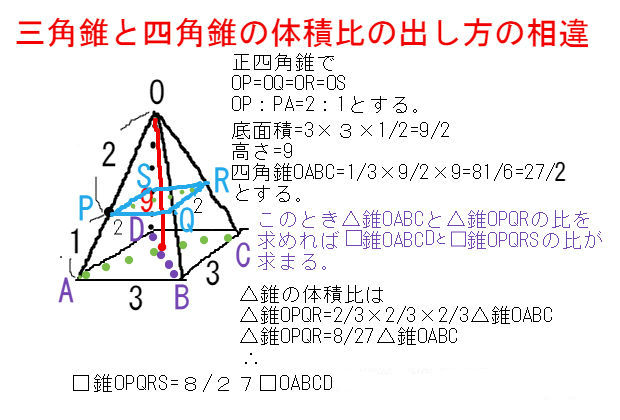



三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト



円錐 すい の表面積や四角錐 五角錐の体積の求め方




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




四角錐の体積の求め方 公式 小学生 中学生の勉強




11月26日 火 角錐の体積の求め方 ノートルダム学院小学校




円錐は1 3 中学生に分かるように真剣に考えてみた うちーノート




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




四角錐の表面積の求め方 公式 小学生 中学生の勉強



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




四角錐の体積




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




角錐 円錐の体積 Youtube



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



この正四角錐の展開図から正四角錐の体積の求め方を教えてください 答えは Yahoo 知恵袋




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
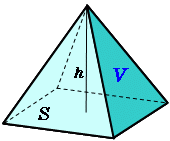



角錐の体積 高精度計算サイト




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧



0 件のコメント:
コメントを投稿